Class 10 NCERT Solutions Physics Chapter 9 - Light: Reflection and Refraction
Light: Reflection and Refraction Exercise 142
Solution 1
Light rays that are parallel to the principal axis of a concave mirror converge at a specific point on its principal axis after reflecting from the mirror. This point is known as the principal focus of the concave mirror.
Solution 2
Radius of curvature, R = 20 cm
Radius of curvature of a spherical mirror = 2 × Focal length (f)
R = 2 f
![]()
Hence, the focal length of the given spherical mirror is 10 cm.
Concept Insight - Always remember that focal length of the spherical mirror is half its radius of curvature.
Solution 3
A concave mirror can give an erect and enlarged image of an object.
Concept insight: When an object is placed between the pole and the principal focus of a concave mirror, the image formed is virtual, erect, and enlarged.
Solution 4
A convex mirror is preferred as a rear-view mirror in vehicles because it gives virtual, erect, and diminished image of the objects placed in front of it. Also, a convex mirror has a wider field of view, which allows the driver to see most of the traffic behind him.
Concept insight: Recall the nature of images formed by convex mirror irrespective of the position of the objects.
Light: Reflection and Refraction Exercise 145
Solution 1
Radius of curvature, R = 32 cm
Radius of curvature = 2 × Focal length (f)
R = 2 f
![]()
Hence, the focal length of the given convex mirror is 16 cm.
Concept Insight - Focal length of a spherical mirror is half the radius of curvature.
Solution 2
Magnification produced by a spherical mirror is given by the relation,

Let the height of the object, hO = h
Then the height of the image, hI = - 3 h (Image formed is real)
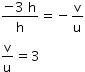
Object distance, u = -10 cm
v = 3 × (-10) = -30 cm
Here, the negative sign indicates that an inverted image is formed at a distance of 30 cm infront of the given concave mirror.
Concept Insight - Following sign conventions in this type of question is very important. Remember that a real image of 3 times the size of the object corresponds to magnification of -3 (note the negative sign).
Light: Reflection and Refraction Exercise 150
Solution 1
The light ray bends towards the normal.
When a ray of light travels from an optically rarer medium to an optically denser medium, it gets bent towards the normal. Since water is optically denser than air, a ray of light travelling from air into the water will bend towards the normal.
Concept insight: Air is rarer medium & water is denser medium. The direction of bending of light depends on whether the light is moving from rarer to denser medium or vice versa.
Solution 2
Refractive index of a medium nm is given by,
![]()
Given:
Speed of light in vacuum, c = 3 × 108 ms-1
Refractive index of glass, ng = 1.50
Speed of light in the glass,
![]()
Concept insight: Remember this formula for refractive index of a medium.
The refractive index of medium 2 with respect to medium 1 is given as,
![]()
The refractive index of medium 1 with respect to medium 2 is given as,
![]()
Solution 3
Highest optical density = Diamond
Lowest optical density = Air
Optical density of a medium is directly related with the refractive index of that medium. A medium which has the highest refractive index will have the highest optical density and vice-versa.
It can be observed from the table that diamond and air respectively have the highest and lowest refractive indices. Therefore, diamond has the highest optical density and air has the lowest optical density.
Solution 4
Speed of light in a medium is given by the relation for refractive index (nm). The relation is given as

It can be inferred from the relation that light will travel the slowest in the material which has the highest refractive index and will travel the fastest in the material which has the lowest refractive index.
It can be observed from the table that the refractive indices of kerosene, turpentine, and water are 1.44, 1.47, and 1.33 respectively. Therefore, light travels the fastest in water.
Concept Insight: Higher is the refractive index of a medium, less is the speed of light in the medium.
Solution 5
Refractive index of a medium nm is related to the speed of light in that medium v by the relation:
![]()
where, c is the speed of light in vacuum/air
The refractive index of diamond is 2.42. This suggests that a light ray travelling in air and entering diamond gets slowed down and its speed becomes ![]() times that in air.
times that in air.
Light: Reflection and Refraction Exercise 158
Solution 1
1 dioptre is defined as the power of a lens of focal length 1 metre.
Solution 2
When an object is placed at the centre of curvature, 2F1, of a convex lens, its image is formed at the centre of curvature, 2F2, on the other side of the lens. The image formed is real, inverted and of the same size as the object, as shown in the given figure.
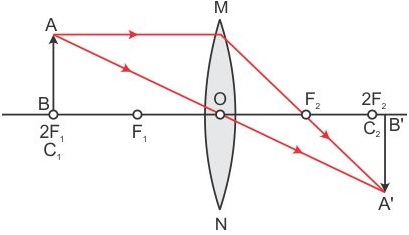
It is given that the image of the needle is formed at a distance of 50 cm from the convex lens. Hence, the needle must be placed in front of the lens at a distance of 50 cm.
Object distance, u = -50 cm
Image distance, v = 50 cm
Focal length = f
According to the lens formula,
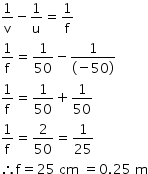
![]()
Hence, the power of the given lens is +4 D.
Concept Insight - One should extremely be careful while substituting the values of u, v and f without forgetting to put the appropriate sign conventions.
Solution 3
Focal length of concave lens, f = -2 m
![]()
Here, negative sign arises due to the divergent nature of concave lens.
Concept Insight:
While using the formula of power, one should be careful to use the value of focal length expressed in meters only.
Light: Reflection and Refraction Exercise Ex. 159
Solution 1
(d) Clay
Concept Insight: A lens allows light to pass through it. Since clay does not show such property, it cannot be used to make a lens.
Solution 2
(d) Between the pole of the mirror and its principal focus.
Concept Insight: When an object is placed between the pole and principal focus of a concave mirror, the image formed is virtual, erect and larger than the object.
Solution 3
(b) At twice the focal length
Concept Insight: When an object is placed at a distance equal to twice the focal length in front of a convex lens, its image is formed at a distance of twice the focal length on the other side of the lens. The image formed is real, inverted, and of the same size as the object.
Solution 4
(a) both concave
Concept Insight: By convention, the focal lengths of a concave mirror and a concave lens are taken as negative. Hence, both, the spherical mirror and the thin spherical lens are concave in nature.
Light: Reflection and Refraction Exercise Ex. 160
Solution 5
(d) either plane or convex
Concept Insight: A convex mirror always gives a virtual and erect image of smaller size than the object placed in front of it. Similarly, a plane mirror always gives a virtual and erect image of same size as that of the object placed in front of it. Therefore, the given mirror could be either plane or convex.
Solution 6
(c) A convex lens of focal length 5 cm.
Concept Insight: A convex lens gives an erect and magnified image of an object when it is placed between the optical centre and focus of the lens. Also, magnification is more for convex lenses having shorter focal length. Therefore, for reading small letters, a convex lens of focal length 5 cm should be used.
Solution 7
Range of object distance = 0 cm to 15 cm
A concave mirror gives an erect image when an object is placed between its pole (P) and the principal focus (F).
Hence, to obtain an erect image of an object from a concave mirror of focal length 15 cm, the object must be placed anywhere between the pole and the focus (i.e. within 15 cm from the mirror). The image formed will be virtual, erect, and magnified in nature, as shown in the given figure.
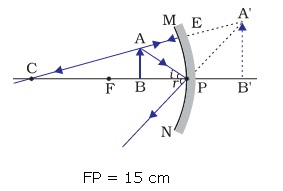
Concept Insight: Recall that in case of concave mirror, the erect & hence the virtual image can be formed only when the object is placed between the principal focus and pole.
Solution 8
(a) Concave (b) Convex (c) Concave
Explanation
(a) Concave mirror is used in the headlights of a car. This is because concave mirrors can produce powerful parallel beam of light when the light source is placed at their principal focus.
(b) Convex mirror is used in side/rear view mirror of a vehicle because convex mirrors give a virtual, erect, and diminished image of the objects placed in front of them and have a wide field of view. It enables the driver to see most of the traffic behind him/her.
(c) Concave mirrors are convergent mirrors. That is why they are used to construct solar furnaces. Concave mirrors converge the light incident on them at a single point known as principal focus. Hence, they can be used to produce a large amount of heat at that point.
Solution 9
The convex lens will form complete image of an object, even if its one-half is covered with black paper. It can be understood by the following two cases.
Case I
When the upper half of the lens is covered:
In this case, the rays of light coming from the object will be refracted by the lower half of the lens. These rays meet at the other side of the lens to form the image of the given object, as shown in the following figure.
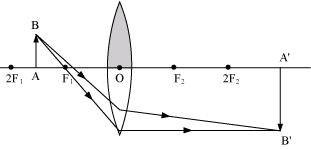
Case II
When the lower half of the lens is covered:
In this case, a ray of light coming from the object is refracted by the upper half of the lens. These rays meet at the other side of the lens to form the image of the given object, as shown in the following figure.
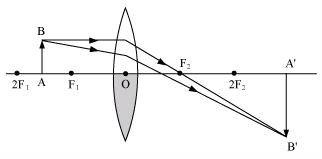
Concept Insight: In case of the half covered lens, the number of rays used up to make the image on the other side of the lens will be reduced to half.
Solution 10
Object distance, u = -25 cm
Object height, ho = 5 cm
Focal length, f = +10 cm
According to the lens formula,
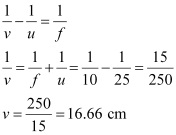
The positive value of v shows that the image is formed at the other side of the lens.
The negative sign shows that the image is real and formed behind the lens.

hi = m x ho = -0.66 x 5 = -3.3 cm
The negative value of image height indicates that the image formed is inverted.
The position, size, and nature of image are shown in the following ray diagram.
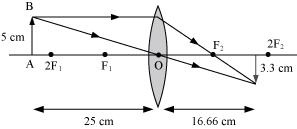
Concept Insight: Remember to use appropriate sign conventions while substituting the values in lens formula.
Solution 11
Focal length (OF1) of the concave lens is f = -15 cm
Image distance, v = -10 cm
According to the lens formula,
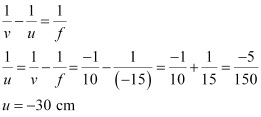
The negative value of u indicates that the object is placed 30 cm in front of the lens. This is shown in the following ray diagram.
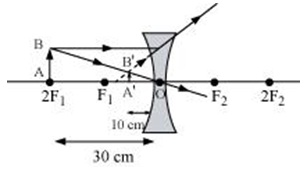
Concept Insight: Remember to use appropriate sign conventions while substituting the values in lens formula.
Solution 12
Focal length of convex mirror, f = +15 cm
Object distance, u = -10 cm
According to the mirror formula,
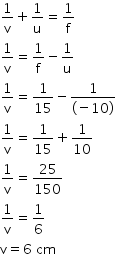
The positive value of v indicates that the image is formed behind the mirror.
![]()
The positive value of magnification indicates that the image formed is virtual and erect.
Concept insight - Correct interpretation of the signs are important.
Remember:
Object distance u is conventionally always taken as negative.
Magnification: Negative value corresponds to real & inverted images. Positive value corresponds to virtual & erect images.
Solution 13
Magnification produced by a mirror is given by,
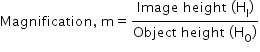
The magnification produced by a plane mirror is +1. It shows that the image formed by the plane mirror is of the same size as that of the object. The positive sign shows that the image formed is virtual and erect.
Concept Insight - Positive magnification corresponds to virtual and erect image. The numeral value of magnification indicates that the size of the image is that many times the size of the object.
Solution 14
Given:
Object distance, u = -20 cm
Object height, H = 5 cm
Radius of curvature, R = 30 cm
Radius of curvature = 2 × Focal length
i.e., R = 2 f
![]()
f = 15 cm
According to the mirror formula,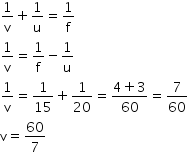
v = 8.57 cm
The positive value of v indicates that the image is formed behind the mirror.
![]()
The positive value of magnification indicates that the image formed is virtual.
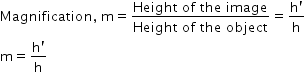
h' = m × h = 0.428 × 5 = 2.14 cm
The positive value of the image height indicates that the image formed is erect.
Therefore, the image formed is virtual, erect and smaller in size.
Concept Insight - Write the given data in appropriate sign conventions. Then identify the unknown quantities that need to be evaluated. Then put the formulae that are most suitable.
Solution 15
Given:
Object distance, u = -27 cm
Object height, h = 7 cm
Focal length, f = -18 cm
According to the mirror formula,
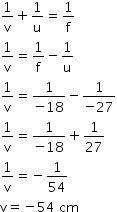
The screen should be placed at a distance of 54 cm in front of the given mirror.

h' = h × m
h' = 7 × (-2) = -14 cm
The negative value of the image height indicates that the image formed is inverted.
Concept Insight - The interpretation of sign convention is the key here.
Solution 16
![]()
P = -2 D
![]()
f = -0.5 m
The focal length is negative. Hence, it is a concave lens.
Concept Insight - The value of the focal length should be written in metres when substituting in the formula:
![]()
Solution 17
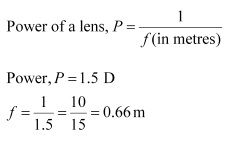
A convex lens has a positive focal length. Hence, it is a convex lens or a converging lens.
Concept Insight: Positive focal length corresponds to convex lens and negative focal length corresponds to concave lens.


