Class 9 NCERT Solutions Maths Chapter 6: Lines And Angles
Ex. 6.1
Ex. 6.2
Lines And Angles Exercise Ex. 6.1
Solution 1

Solution 2
Let common ratio between a and b is x, a = 2x and b = 3x.
XY is a straight line, OM and OP rays stands on it.
XOM + MOP + POY = 180 b + a + POY = 180
3x + 2x + 90 = 180
5x = 90
x = 18
a = 2x
= 2 * 18
= 36
b = 3x
= 3 * 18
= 54
Now, MN is a straight line. OX ray stands on it.
![]() b +
b + ![]() c = 180
c = 180
54 + ![]() c = 180
c = 180
![]() c = 180 54 = 126
c = 180 54 = 126
![]() c = 126
c = 126
Solution 3
In the given figure, ST is a straight line and QP ray stand on it.
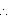
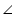 PQS +
PQS + 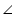 PQR = 180 (Linear Pair)
PQR = 180 (Linear Pair)
Given that
180 -
Solution 4
We may observe that
x + y + z + w = 360 (Complete angle)
It is given that
x + y = z + w
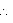 x + y + x + y = 360
x + y + x + y = 360
x + y + z + w = 360 (Complete angle)
It is given that
x + y = z + w
2(x + y) = 360
x + y = 180
Since x and y form a linear pair, thus AOB is a line.
Solution 5
Given that OR 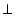 PQ
PQ
On adding equations (1) and (2), we have
2 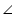 ROS =
ROS = 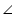 QOS -
QOS - 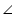 POS
POS
Solution 6
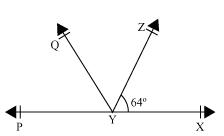
Given that line YQ bisects  PYZ.
PYZ.
Hence, QYP =
QYP =  ZYQ
ZYQ
Now we may observe that PX is a line. YQ and YZ rays stand on it.
Hence,
Now we may observe that PX is a line. YQ and YZ rays stand on it.
Also, 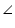 ZYQ =
ZYQ = 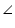 QYP = 58
QYP = 58
Reflex 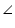 QYP = 360o - 58o = 302o
QYP = 360o - 58o = 302o
= 64o + 58o = 122o
Lines And Angles Exercise Ex. 6.2
Solution 1
Given that AB || CD and CD || EF
Now we may observe that
x = z (alternate interior angles) ... (1)
Given that y: z = 3: 7
Let common ratio between y and z be a
 y = 3a and z = 7a
y = 3a and z = 7a
x = z (alternate interior angles) ... (1)
Given that y: z = 3: 7
Let common ratio between y and z be a
Also x + y = 180 (co-interior angles on the same side of the transversal)
z + y = 180 [Using equation (1)]
7a + 3a = 180
10a = 180
a = 18
 x = 7 a = 7
x = 7 a = 7 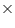 18 = 126
18 = 126
Solution 2
It is given that
AB || CD
AB || CD
EF 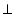 CD
CD
GED = 126
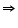
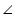 GEF +
GEF + 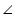 FED = 126
FED = 126
Now,
But  AGE +
AGE + FGE = 180 (linear pair)
FGE = 180 (linear pair)
Solution 3
Let us draw a line XY parallel to ST and passing through point R.
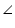 PQR +
PQR + 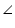 QRX = 180 (co-interior angles on the same side of transversal QR)
QRX = 180 (co-interior angles on the same side of transversal QR)
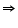 110 +
110 + 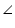 QRX = 180
QRX = 180
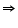
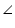 QRX = 70
QRX = 70
Now,
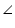 RST +
RST +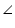 SRY = 180 (co-interior angles on the same side of transversal SR)
SRY = 180 (co-interior angles on the same side of transversal SR)
130 +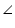 SRY = 180
SRY = 180
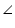 SRY = 50
SRY = 50
XY is a straight line. RQ and RS stand on it.
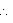
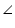 QRX +
QRX + 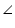 QRS +
QRS +  SRY = 180
SRY = 180
70 + QRS + 50 = 180
QRS + 50 = 180
 QRS = 180 - 120 = 60
QRS = 180 - 120 = 60
Now,
130 +
XY is a straight line. RQ and RS stand on it.
70 +
Solution 4
50 + y = 127
y = 127 - 50
y = 77
Also
50 = x
Solution 5
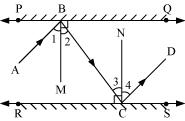
Let us draw BM  PQ and CN
PQ and CN  RS.
RS.
As PQ || RS
So, BM || CN
Thus, BM and CN are two parallel lines and a transversal line BC cuts them at B and C respectively.
As PQ || RS
So, BM || CN
Thus, BM and CN are two parallel lines and a transversal line BC cuts them at B and C respectively.
But 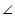 1 =
1 = 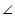 2 and
2 and 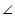 3 =
3 = 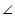 4 (By laws of reflection)
4 (By laws of reflection)
Now, 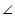 1 +
1 + 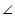 2 =
2 = 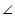 3 +
3 + 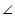 4
4
But, these are alternate interior angles
