Class 9 NCERT Solutions Physics Chapter 7: Motion
Motion Exercise 74
Solution 1
Yes. An object that has moved through a distance can have zero displacement. Displacement is the shortest distance between the initial and the final position of an object. An object which has covered a distance can have zero displacement if it comes back to its starting point i.e., the initial position.
Consider the following situation. A man is walking along the boundary of a square park of side 20 m (as shown in the following figure). He starts walking from point A and after moving along all the sides of the park (AB, BC, CD, DA), he again comes back to the same point i.e., A.
In this case, the total distance covered by the man is 20 m + 20 m + 20 m + 20 m = 80 m. However, his displacement is zero because the shortest distance between his initial and final position is zero.
Solution 2
In 2 min and 20 s (140 s), he will cover a distance =
= 140 mTherefore, the farmer completes
=3.5 rounds (3 complete rounds and a half round) of the field in 2 min and 20 s. That means, after 2 min 20 s, the farmer will be at the opposite end of the starting point.
Now, there can be two extreme cases.
Case I: Starting point is a corner point of the field.
In this case, the farmer will be at the diagonally opposite corner of the field after 2 min 20 s.
Therefore, the displacement will be equal to the diagonal of the field.
Hence, the displacement will be
= 14.14 mCase II: Starting point is the middle point of any side of the field.
In this case the farmer will be at the middle point of the opposite side of the field after 2 min 20 s.
Therefore, the displacement will be equal to the side of the field, i.e., 10 m.
For any other starting point, the displacement will be between 14.1 m and 10 m.
Concept Insight: - Be careful about considering the cases, as the displacement in both the cases is different.
Solution 3
Displacement can become zero when the initial and final positions of the object are the same.
Concept Insight - Displacement is always less than or equal to the distance covered.
Motion Exercise 76
Solution 1
|
Speed |
Velocity |
|
Speed is the distance travelled by an object per unit time. It does not have any direction. |
Velocity is the displacement of an object per unit time. It has a unique direction. |
|
Speed is a scalar quantity. |
Velocity is a vector quantity. |
|
The speed of an object can never be negative. At the most, it can become zero. This is because distance travelled can never be negative. |
The velocity of an object can be negative, positive, or equal to zero. This is because displacement can take any of these three values. |
Solution 2
If the total distance covered by an object is the same as its displacement, then its average speed would be equal to its average velocity, i.e. when the object moves along a straight line path.
Concept Insight - Distance and displacement may or may not be equal to each other.
Solution 3
Solution 4
Solution 5
= 5 min = 5 × 60 = 300 s
Concept Insight - Convert all the quantities in the same units and then proceed to calculations.
Motion Exercise 77
Solution 1
(i) A body is said to have uniform acceleration if it travels in a straight path in such a way that its velocity changes at a uniform rate, i.e., the velocity of the body increases or decreases by equal amounts in an equal intervals of time. The motion of a freely falling body is an example of uniform acceleration.
(ii) A body is said to have non-uniform acceleration if its velocity changes at a non-uniform rate, i.e., the velocity of the body increases or decreases by unequal amounts in an equal intervals of time. The motion of a car on a crowded city road is an example of non-uniform acceleration.
Solution 2
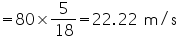
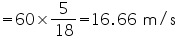
Solution 3
Time taken, t = 10 min = 
Motion Exercise 81
Solution 1
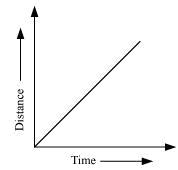
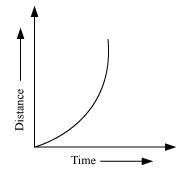
Solution 2
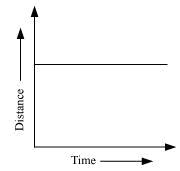
Solution 3
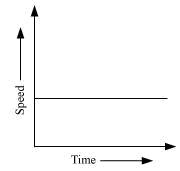
Solution 4
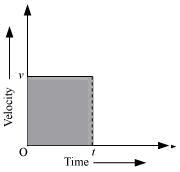
Let the velocity of the body at time (t) be v.
Area of the shaded region = length × breath
Length = t
Breath = v
Area = vt = velocity × time ...(i)
We know,
Distance = Velocity x Time ...(ii)Hence, the area occupied below the velocity-time graph measures the distance covered by the body.
Motion Exercise 82
Solution 1
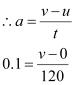
(12)2 - (0)2 = 2(0.1) s
So, speed acquired by the bus is 12 m/s.
Distance travelled by the bus is 720 m.
Solution 2
Solution 3
Acceleration, a = 2 cm s-2 = 0.02 m/s2
Time, t = 3s
According to the first equation of motion:
v = u + at
Concept Insight - Choose the equation of motion wisely out of the three, to minimize the number of steps in calculations.
where, v is the velocity of the trolley after 3s from start
v = 0 + 0.02 × 3 = 0.06 m/s
Hence, the velocity of the trolley after 3s from start is 0.06 m/s.
Motion Exercise 83
Solution 4
Acceleration, a = 4 m/s2
Time taken, t = 10 s
According to the second equation of motion:
where, s is the distance covered by the racing car
Solution 5
Final velocity, v = 0 (since the stone comes to rest when it reaches its maximum height)
Acceleration of the stone, a = acceleration due to gravity, g = 10 m/s2 (in downward direction)
There will be a change in the sign of acceleration because the stone is being thrown upwards.
Concept Insight - Change in sign of the acceleration due to change in direction is crucial as it'll change the results.
Acceleration, a = -10 m/s2
Let s be the maximum height attained by the stone in time t.
According to the first equation of motion:
v = u + at
0 = 5 + (-10) t
v 2 = u 2 + 2 as
(0) 2 = (5) 2 + 2(-10) s
Motion Exercise 85
Solution 1
r = 2(100) = 200 m Concept Insight - Circumference of a circle is given by (2 ×
× r) where, r is the radius of the circle and = 22/7.In 40 s, the given athlete covers a distance of 200
m. In 1 s, the given athlete covers a distance =
m
=2200 mThe athlete covers one round of the circular track in 40 s. This means that after every 40 s, the athlete comes back to his original position. Hence, in 140 s he had completed 3 rounds of the circular track and is taking the fourth round.
He takes 3 rounds in 40 × 3 = 120 s. Thus, after 120s his displacement is zero.
Then, the net displacement of the athlete is in 20 s only. In this interval of time, he moves at the opposite end of the initial position. Since displacement is equal to the shortest distance between the initial and final position of the athlete, displacement of the athlete will be equal to the diameter of the circular track.
Displacement of the athlete = 200 m
Distance covered by the athlete in 2 min 20 s is 2200 m and his displacement is 200 m.
Solution 2
= 2 m/s
= 1.90 m/s
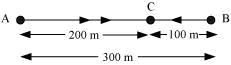
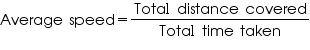
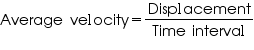
= 0.95 m/sSolution 3
.... (i)
.... (ii)
From equations (i) and (ii),
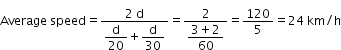
Solution 4
Acceleration of the motorboat, a = 3 m/s2
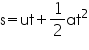
Solution 5
For first car:
Initial speed of the car, u1 = 52 km/h = 
= 14.4 m/s
Time taken to stop the car, t1 = 5 s
Final speed of the car becomes zero after 5s of application of brakes.
For second car:
Initial speed of the car, u2 = 3 km/h = 
= 0.83 m/s
Time taken to stop the car, t2 = 10 s
Final speed of the car becomes zero after 10 s of application of brakes.
Plot of the speed versus time graph for the two cars is shown in the following figure:
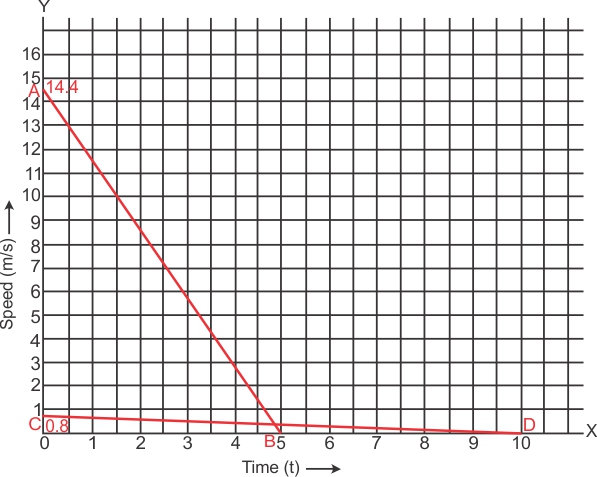
Distance covered by first car = Area under the graph line AB
= Area of triangle OAB
= 
= 36 m
Distance covered by second car = Area under the graph line CD
= Area of triangle OCD
= 
= 4.15 m
Area of triangle OAB > Area of triangle OCD
Thus, the distance covered by first car is greater than the distance covered by second car.
Hence, the car travelling with a speed of 52 km/h travelled farther after brakes were applied.
Solution 6
(b) The distance-time graphs of the three objects A, B and C never meet at a single point. Thus, they are never at the same point on the road.
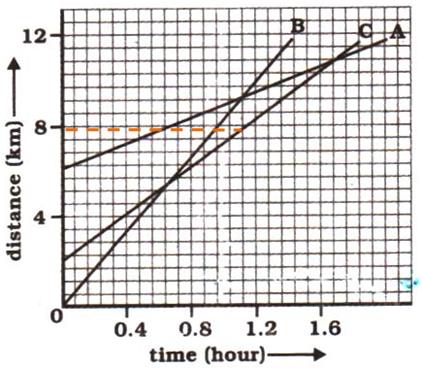
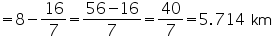
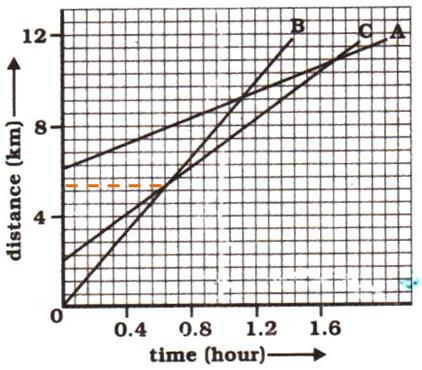
Hence, B has travelled a distance of 5.143 km when it passes C.
Motion Exercise 86
Solution 7
Acceleration, a = 10 m/s2
Initial velocity, u = 0 (since the ball was initially at rest)
Final velocity of the ball with which it strikes the ground, v
According to the third equation of motion:
v 2 = u 2 + 2 as
v 2 = 0 + 2 (10) (20)
v = 20 m/s
Concept Insight - Choose the equation of motion wisely out of the three, to minimize the number of steps in calculations.
The ball will strike the ground with a velocity 20 m/s.
According to the first equation of motion:
v = u + at
20 = 0 + 10 (t)
t = 2s
Hence, the ball will strike the ground after 2s with a velocity of 20 m/s.
Solution 8
(a) The distance travelled by the car in the first 4 seconds is given by the area between the curve and the time axis from t = 0 to t = 4 s. This area has been shaded in the graph below.
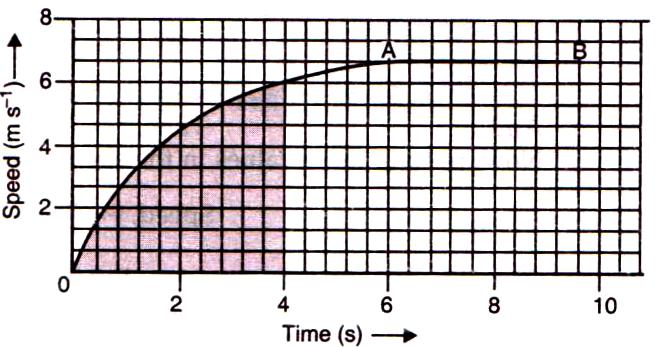
Number of squares in the shaded part of the graph = 62
Concept Insight: While counting the number of squares in the shaded part of the graph, the squares which are half or more than half are counted as complete squares but the squares which are less than half are not counted.
On X-axis,
5 squares represent 2 s.
1 square represents 
s.
On Y-axis,
3 squares represent 2 m/s.
1 square represents 
m/s.
So, area of 1 square on the graph = 
Area of the shaded region of the graph = 
Therefore, the car travels a distance of 16.53 m in the first 4 seconds.
(b) The uniform motion of the car is represented by the part AB of the graph, which represents constant speed.
Solution 9
When a car is moving in a circular track, its acceleration is perpendicular to its direction of motion at each instant.
Solution 10
x r) where, r is the radius of the circle and = 22/7 = 3.14Speed of an object moving in a circular orbit,
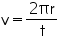
Hence, the speed of the artificial satellite is 3.07 km/s
