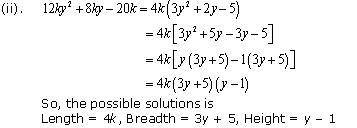Class 9 NCERT Solutions Maths Chapter 2: Polynomials
Polynomials Exercise Ex. 2.1
Solution 1
Yes, this expression is a polynomial in one variable x.
(ii)
Yes, this expression is a polynomial in one variable y.
(iii)
No, here the exponent of variable t in term which is not a whole number.
So this expression is not a polynomial.
(iv)
No, here the exponent of variable t in term ![]() is -1, which is not a whole number. So this expression is not a polynomial.
is -1, which is not a whole number. So this expression is not a polynomial.
(v)
No, this expression is a polynomial in 3 variables x, y and t.
Concept Insight: In such problems to check whether the given algebraic expressions is a polynomial or not, check the exponents of variable to be a whole number. The second step is to look for the number of variables the expression has. Any alphabet used in the expression is the variable unless specified as constant.
Solution 2
Solution 3
Solution 4
Solution 5
(ii) x - x3 is a cubic polynomial as its degree is 3.
(iii) y + y2 + 4 is a quadratic polynomial as its degree is 2.
(iv) 1 + x is a linear polynomial as its degree is 1.
(v) 3t is a linear polynomial as its degree is 1.
(vi) γ2 is a quadratic polynomial as its degree is 2.
(vii) 7x3 is a cubic polynomial as its degree is 3.
Polynomials Exercise Ex. 2.2
Solution 1
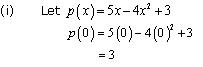
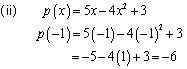
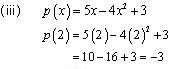
Solution 2
p(0) = (0)2 - (0) + 1 = 1
p(1) = (1)2 - (1) + 1 = 1
p(2) = (2)2 - (2) + 1 = 3
p(0) = 2 + 0 + 2 (0)2 - (0)3 = 2
p(1) = 2 + (1) + 2(1)2 - (1)3
= 2 + 1 + 2 - 1 = 4
= 2 + 2 + 8 - 8 = 4
p(0) = (0)3 = 0
p(1) = (1)3 = 1
p(2) = (2)3 = 8
p(0) = (0 - 1) (0 + 1) = (- 1) (1) = - 1
p(1) = (1 - 1) (1 + 1) = 0 (2) = 0
p(2) = (2 - 1 ) (2 + 1) = 1(3) = 3
Solution 3

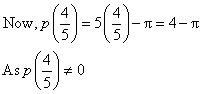
Now, p(1) = (1)2 - 1 = 0
p(- 1) = (- 1)2 - 1 = 0
Hence x = 1 and - 1 are zeroes of polynomial.
Now, p(- 1) = (- 1 + 1) (- 1 - 2) = 0 (-3) = 0
p(2) = (2 + 1) (2 - 2 ) = 3 (0) = 0
So, x = - 1 and x = 2 are zeroes of given polynomial.
Now, p(0) = (0)2 = 0
Hence x = 0 is a zero of given polynomial

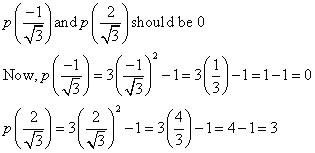
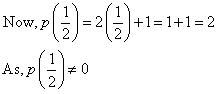
Solution 4
(i) p(x) = x + 5
p(x) = 0
x + 5 = 0
x = - 5
So, for x = - 5, value of polynomial is 0 and hence x = - 5 is a zero of polynomial.
p(x) = 0
x - 5 = 0
x = 5
So, for x = 5 value of polynomial is 0 and hence x = 5 is a zero of polynomial.
p(x) = 0
2x + 5 = 0
2x = - 5
So, for
p(x) = 0
3x - 2 = 0
So, for
p(x) = 0
3x = 0
x = 0
So, for x = 0 value of polynomial is 0 and hence x = 0 is a zero of polynomial.
p(x) = 0
ax = 0
x = 0
So, for x = 0, value of polynomial is 0. Hence x = 0 is a zero of polynomial.
p(x) = 0
cx+ d = 0
Polynomials Exercise Ex. 2.3
Solution 1
Here, p(x) = x3 + x2 + x + 1
p(-1) = (- 1)3 + (- 1)2 + (- 1) + 1
= - 1 + 1 - 1 + 1 = 0
Hence, x + 1 is a factor of this polynomial
Here, p(x) = x4 + x3 + x2 + x + 1
p( -1) = (- 1)4 + (- 1)3 + (- 1)2 + (- 1) + 1
= 1 - 1 + 1 -1 + 1 = 1
As,
p(- 1) = (- 1)4 + 3(- 1)3 + 3(- 1)2 + (- 1) + 1
= 1 - 3 + 3 - 1 + 1 = 1
As,
p(x) =
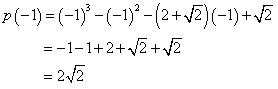
As,
So, (x + 1) is not a factor of this polynomial.
Solution 2
p(x) = 2x3 + x2 - 2x - 1
p(- 1) = 2(- 1)3 + (- 1)2 - 2(- 1) - 1
= 2(- 1) + 1 + 2 - 1 = 0
Hence, g(x) = x + 1 is a factor of given polynomial.
p(x) = x3 +3x2 + 3x + 1
p(- 2) = (- 2)3 + 3(- 2)2 + 3(- 2) + 1
= - 8 + 12 - 6 + 1
= - 1
Hence g(x) = x + 2 is not a factor of given polynomial.
p(x) = x3 - 4 x2 + x + 6
p(3) = (3)3 - 4(3)2 + 3 + 6
= 27 - 36 + 9 = 0
So, g(x) = x - 3 is a factor of given polynomial.
Solution 3
p(1) = 0
So, value of k is - 2.
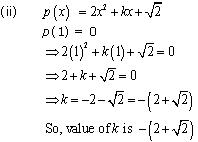
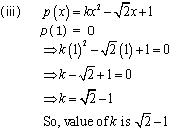
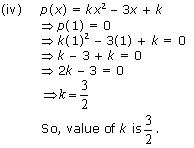
Solution 4
The two numbers such that pq = 12
Now, 12x2 - 7x + 1 = 12x2 - 4x - 3x + 1
= 4x (3x - 1) - 1 (3x - 1)
= (3x - 1) (4x - 1)
The two numbers such that pq = 2
They are p = 6 and q = 1
Now, 2x2 + 7x + 3 = 2x2 + 6x + x + 3
= 2x (x + 3) + 1 (x + 3)
= (x + 3) (2x+ 1)
The two numbers such that pq = - 36 and p + q = 5.
They are p = 9 and q = - 4
Now,
6x2 + 5x - 6 = 6x2 + 9x - 4x - 6
= 3x (2x + 3) - 2 (2x + 3)
= (2x + 3) (3x - 2)
(iv) 3x2 - x - 4
The two numbers such that pq = 3
They are p = - 4 and q = 3.
Now,
3x2 - x - 4 = 3x2 - 4x + 3x - 4
= x (3x - 4) + 1 (3x - 4)
= (3x - 4) (x + 1)
b is expressed as the sum of two numbers whose product is ac.
Do not forget to consider the sign of the terms while splitting.
Remember
|
ac>0 |
b>0 |
b =(p+q) where p>0,q>0 |
|
ac>0 |
b<0 |
b =(p+q) where p<0,q<0 |
|
ac<0 |
b>0 |
b =(p+q) where |
|
ac<0 |
b<0 |
b =(p+q) where |
Solution 5
Factors of 2 are 1, 2.
By hit and trial method
p(2) = (2)3 - 2(2)2 - 2 + 2
= 8 - 8 - 2 + 2 = 0
So, (x - 2) is factor of polynomial p(x)
By long division

= (x + 1) [x2 - 2x - x + 2]
= (x + 1) [x (x - 2) - 1 (x - 2)]
= (x + 1) (x - 1) (x - 2)
= (x - 2) (x - 1) (x + 1)
Factors of 5 are 1, 5.
By hit and trial method
p(- 1) = (- 1)3 - 3(- 1)2 - 9(- 1) - 5
= - 1 - 3 + 9 - 5 = 0
So x + 1 is a factor of this polynomial
Let us find the quotient while dividing x3 + 3x2 - 9x - 5 by x + 1
By long division
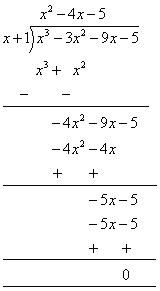
= (x + 1) (x2 - 5 x + x - 5)
= (x + 1) [(x (x - 5) +1 (x - 5)]
= (x + 1) (x - 5) (x + 1)
= (x - 5) (x + 1) (x + 1)
The factors of 20 are 1, 2, 4, 5 ... ...
By hit and trial method
p(- 1) = (- 1)3 + 13(- 1)2 + 32(- 1) + 20
= - 1 + 13 - 32 + 20
= 33 - 33 = 0
As p(-1) is zero, so x + 1 is a factor of this polynomial p(x).
Let us find the quotient while dividing x3 + 13x2 + 32x + 20 by (x + 1)
By long division
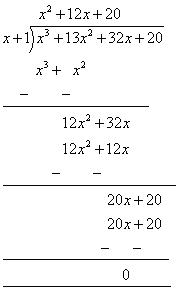
Dividend = Divisor
x3 + 13x2 + 32x + 20 = (x + 1) (x2 + 12x + 20) + 0
= (x + 1) (x2 + 10x + 2x + 20)
= (x + 1) [x (x + 10) + 2 (x + 10)]
= (x + 1) (x + 10) (x + 2)
= (x + 1) (x + 2) (x + 10)
By hit and trial method
p(1) = 2 ( 1)3 + (1)2 - 2( 1) - 1
= 2 + 1 - 2 - 1= 0
So, y - 1 is a factor of this polynomial
By long division method,
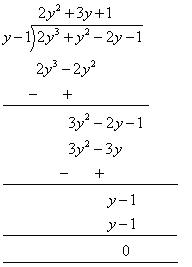
= (y - 1) (2y2 +3y + 1)
= (y - 1) (2y2 +2y + y +1)
= (y - 1) [2y (y + 1) + 1 (y + 1)]
= (y - 1) (y + 1) (2y + 1)
Check the obtained factors for the possible zeroes of the polynomial p(x) Using Factor theorem one zero can be obtained continue the process till all the zeroes are obtained or use long division method. To obtain the other quadratic factor use long division to determine the other factors. The degree of the polynomial is less than or equal to the number of real factors the polynomial.
Polynomials Exercise Ex. 2.4
Solution 1

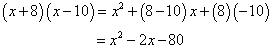
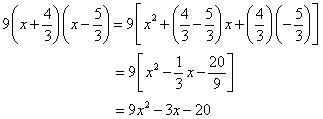

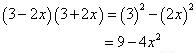
Solution 2
= (100)2 + (3 + 7) 100 + (3) (7)
[By using the identity,
= 10000 + 1000 + 21
= 11021
= (100)2 + (- 5 - 4) 100 + (- 5) (- 4)
[By using the identity,
x = 100, a = - 5 and b = - 4]
= 10000 - 900 + 20
= 9120
= (100)2 - (4)2
= 10000 - 16
= 9984
Solution 3
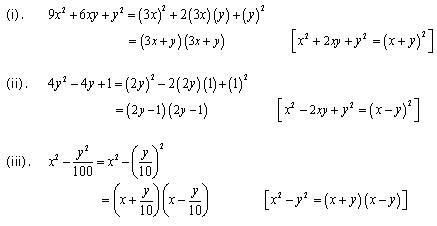
Solution 4
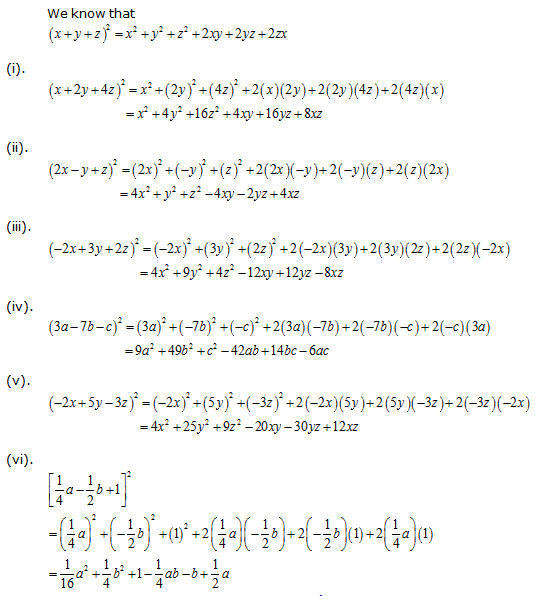
Solution 5
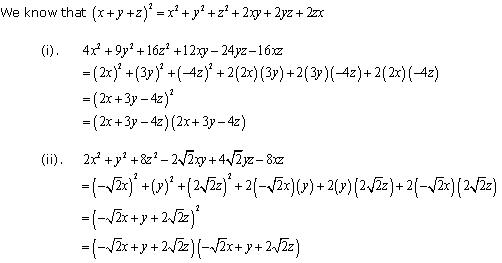
Solution 6
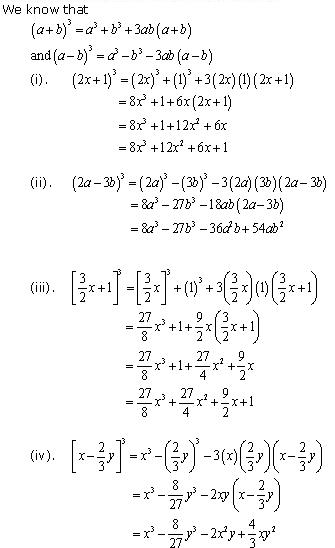
Solution 7
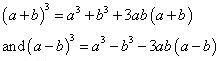
= (100)3 - (1)3 - 3(100) (1) (100 - 1)
= 1000000 - 1 - 300(99)
= 1000000 - 1 - 29700
= 970299
(ii) (102)3 = (100 + 2)3
= (100)3 + (2)3 + 3(100) (2) (100 + 2)
= 1000000 + 8 + 600 (102)
= 1000000 + 8 + 61200
= 1061208
(iii) (998)3 = (1000 - 2)3
= (1000)3 - (2)3 - 3(1000) (2) (1000 - 2)
= 1000000000 - 8 - 6000(998)
= 1000000000 - 8 - 5988000
= 1000000000 - 5988008
= 994011992
Solution 8

Solution 9
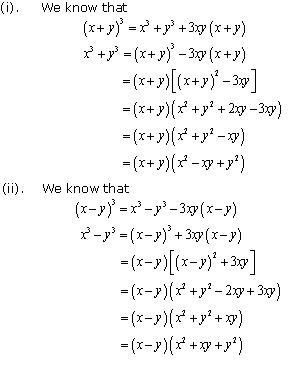
Solution 10

Solution 11
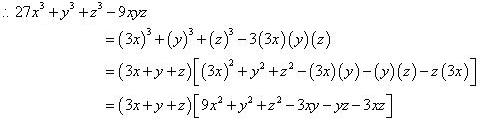
Solution 12
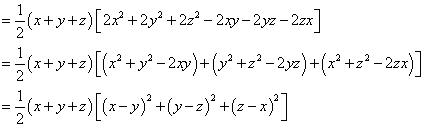
Solution 13

Solution 14
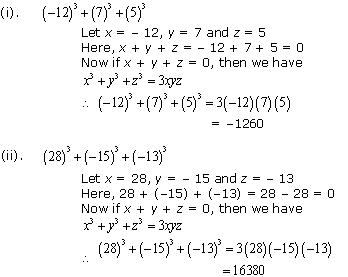
Solution 15
Area = length
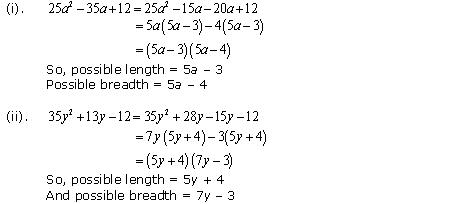
Solution 16
Volume of cuboid = length
So, the possible solutions is
Length = 3, breadth = x, height = x - 4