Class 9 NCERT Solutions Maths Chapter 8: Quadrilaterals
Ex. 8.1
Ex. 8.2
Quadrilaterals Exercise Ex. 8.1
Solution 1
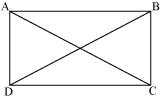
Let ABCD be a parallelogram. To show ABCD a rectangle, only we need to prove one of its interior angle is 90.
In ABC and
ABC and  DCB
DCB
AB = DC (opposite sides of a parallelogram are equal)
BC = BC (common)
AC = DB (given)
 ABC
ABC  DCB (by SSS Congruence rule)
DCB (by SSS Congruence rule)
In
AB = DC (opposite sides of a parallelogram are equal)
BC = BC (common)
AC = DB (given)
We know that sum of measures of angles on the same side of transversal is 180º.
Since ABCD is a parallelogram and one of its interior angles is 90, therefore, ABCD is rectangle.
Solution 2
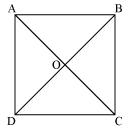
Let ABCD be a square. Let the diagonals AC and BD intersect each other at a point O.
To show diagonals of a square are equal and bisect each other at right angles, we need to prove AC = BD, OA = OC, OB = OD and AOB = 90
AOB = 90
Now, in ABC and
ABC and  DCB
DCB
AB = DC (sides of square are equal to each other)
 ABC =
ABC =  DCB (all interior angles are of 90 )
DCB (all interior angles are of 90 )
BC = BC (common side)
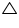 ABC
ABC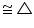 DCB (by SAS congruency)
DCB (by SAS congruency)
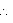 AC = DB (by CPCT)
AC = DB (by CPCT)
To show diagonals of a square are equal and bisect each other at right angles, we need to prove AC = BD, OA = OC, OB = OD and
Now, in
AB = DC (sides of square are equal to each other)
BC = BC (common side)
Hence, the diagonals of a square are equal in length
Now in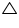 AOB and
AOB and 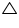 COD
COD
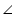 AOB =
AOB = 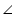 COD (vertically opposite angles)
COD (vertically opposite angles)
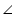 ABO =
ABO = 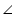 CDO (alternate interior angles)
CDO (alternate interior angles)
AB = CD (sides of square are always equal)
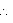
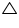 AOB
AOB 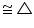 COD (by AAS congruence rule)
COD (by AAS congruence rule)
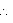 AO = CO and OB = OD (by CPCT)
AO = CO and OB = OD (by CPCT)
Now in
AB = CD (sides of square are always equal)
Hence, the diagonals of a square bisect each other
Now in
Now as we had proved that diagonals bisect each other
So, AO = CO
AB = CB (sides of square are equal)
BO = BO (common)
But,
2
Hence, the diagonals of a square bisect each other at right angle.
Solution 3
(i) ABCD is a parallelogram.
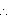
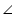 DAC =
DAC = 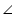 BCA (Alternate interior angles) ... (1)
BCA (Alternate interior angles) ... (1)
And 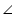 BAC =
BAC = 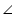 DCA (Alternate interior angles) ... (2)
DCA (Alternate interior angles) ... (2)
But it is given that AC bisects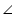 A.
A.
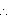
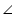 DAC =
DAC = 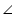 BAC ... (3)
BAC ... (3)
But it is given that AC bisects
From equations (1), (2) and (3), we have
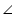 DAC =
DAC = 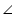 BCA =
BCA = 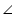 BAC =
BAC = 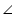 DCA ... (4)
DCA ... (4)
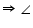 DCA =
DCA = 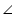 BCA
BCA
Hence, AC bisects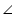 C.
C.
(ii)
Hence, AC bisects
(ii)
From equation (4), we have
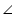 DAC =
DAC = 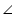 DCA
DCA
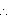 DA = DC (side opposite to equal angles are equal)
DA = DC (side opposite to equal angles are equal)
But DA = BC and AB = CD (opposite sides of parallelogram)
Hence, ABCD is rhombus
Solution 4
(i)
Given:
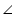 DAC =
DAC = and 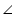 DCA =
DCA = 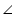 BCA ... (2)
BCA ... (2)
Now, AD || BC and AC is a transversal
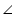 CAB =
CAB = In ΔABC, we have
 BC = AB ... (Sides opposite to equal angles are equal)
BC = AB ... (Sides opposite to equal angles are equal)But BC = AD and AB = CD ... Since ABCD is a rectangle.
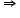 AB = BC = AD = CD
AB = BC = AD = CDAll the sides of this rectangle are equal.
Thus, ABCD is a square.
(ii)
Since, ABCD is a square and we know that the diagonals of a square bisect its angles.
Solution 5
(i) In  APD and
APD and  CQB
CQB
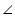 ADP =
ADP = 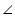 CBQ (alternate interior angles for BC || AD)
CBQ (alternate interior angles for BC || AD)
AD = CB (opposite sides of parallelogram ABCD)
DP = BQ (given)
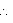
 APD
APD 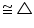 CQB (using SAS congruence rule)
CQB (using SAS congruence rule)
(ii) As we had observed that APD
APD 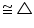 CQB
CQB
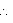 AP = CQ (CPCT)
AP = CQ (CPCT)
AD = CB (opposite sides of parallelogram ABCD)
DP = BQ (given)
(ii) As we had observed that
(iii) In  AQB and
AQB and  CPD
CPD
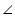 ABQ =
ABQ =  CDP (alternate interior angles for AB || CD)
CDP (alternate interior angles for AB || CD)
AB = CD (opposite sides of parallelogram ABCD)
BQ = DP (given)
 AQB
AQB CPD (using SAS congruence rule)
CPD (using SAS congruence rule)
(iv) As we had observed that AQB
AQB CPD
CPD
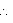 AQ = CP (CPCT)
AQ = CP (CPCT)
AB = CD (opposite sides of parallelogram ABCD)
BQ = DP (given)
 AQB
AQB(iv) As we had observed that
(v) From the result obtained in (ii) and (iv), we have
AQ = CP and AP = CQ
Since opposite sides in quadrilateral APCQ are equal to each other. So, APCQ is a
parallelogram.
Solution 6
(i) In 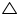 APB and
APB and 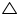 CQD
CQD
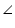 APB =
APB = 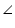 CQD (each 90o)
CQD (each 90o)
AB = CD (opposite sides of parallelogram ABCD)
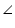 ABP =
ABP = 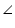 CDQ (alternate interior angles for AB || CD)
CDQ (alternate interior angles for AB || CD)
 APB
APB 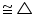 CQD (by AAS congruency)
CQD (by AAS congruency)
(ii) By using the result obtained as above
 APB
APB  CQD, we have
CQD, we have
AP = CQ (by CPCT)
AB = CD (opposite sides of parallelogram ABCD)
(ii) By using the result obtained as above
AP = CQ (by CPCT)
Solution 7
Extend AB. Draw a line through C, which is parallel to AD, intersecting AE at point E.
Now, AECD is a parallelogram.
Now, AECD is a parallelogram.
(i) AD = CE (opposite sides of parallelogram AECD)
But AD = BC (given)
So, BC = CE
 CEB =
CEB =  CBE (angle opposite to equal sides are also equal)
CBE (angle opposite to equal sides are also equal)
Now consider parallel lines AD and CE. AE is transversal line for them
 A +
A +  CEB = 180 (angles on the same side of transversal)
CEB = 180 (angles on the same side of transversal)
 A+
A+  CBE = 180 (using the relation
CBE = 180 (using the relation CEB =
CEB =  CBE) ... (1)
CBE) ... (1)
But B +
B +  CBE = 180 (linear pair angles) ... (2)
CBE = 180 (linear pair angles) ... (2)
From equations (1) and (2), we have
 A =
A =  B
B
(ii) AB || CD
 A +
A +  D = 180 (angles on the same side of transversal)
D = 180 (angles on the same side of transversal)
Also C +
C +  B = 180 (angles on the same side of transversal)
B = 180 (angles on the same side of transversal)
 A +
A +  D =
D =  C +
C +  B
B
But AD = BC (given)
So, BC = CE
Now consider parallel lines AD and CE. AE is transversal line for them
But
From equations (1) and (2), we have
(ii) AB || CD
Also
But
(iii) In ABC and BAD
AB = BA (common side)
BC = AD (given)
(iv)
Quadrilaterals Exercise Ex. 8.2
Solution 1
(i) In  ADC, S and R are the mid points of sides AD and CD respectively.
ADC, S and R are the mid points of sides AD and CD respectively.
In a triangle the line segment joining the mid points of any two sides of the triangle is
In a triangle the line segment joining the mid points of any two sides of the triangle is
parallel to the third side and is half of it.
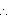 SR || AC and SR =
SR || AC and SR = 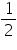 AC ... (1)
AC ... (1)
(ii) In ABC, P and Q are mid points of sides AB and BC respectively. So, by using
(ii) In ABC, P and Q are mid points of sides AB and BC respectively. So, by using
mid-point theorem, we have
PQ || AC and PQ =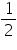 AC ... (2)
AC ... (2)
Now using equations (1) and (2), we have
PQ || SR and PQ = SR ... (3)
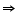 PQ = SR
PQ = SR
(iii) From equations (3), we have
PQ || SR and PQ = SR
Clearly one pair of opposite sides of quadrilateral PQRS is parallel and equal
Hence, PQRS is a parallelogram.
PQ || AC and PQ =
Now using equations (1) and (2), we have
PQ || SR and PQ = SR ... (3)
(iii) From equations (3), we have
PQ || SR and PQ = SR
Clearly one pair of opposite sides of quadrilateral PQRS is parallel and equal
Hence, PQRS is a parallelogram.
Solution 2
In  ABC, P and Q are mid points of sides AB and BC respectively.
ABC, P and Q are mid points of sides AB and BC respectively.
 PQ || AC and PQ =
PQ || AC and PQ =  AC (using mid-point theorem) ... (1)
AC (using mid-point theorem) ... (1)
In
R and S are the mid points of CD and AD respectively
From equations (1) and (2), we have
PQ || RS and PQ = RS
As in quadrilateral PQRS one pair of opposite sides are equal and parallel to each other, so, it is a parallelogram.
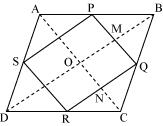
Let diagonals of rhombus ABCD intersect each other at point O.
Now in quadrilateral OMQN
MQ || ON (
QN || OM (
So, OMQN is parallelogram
But,
Clearly PQRS is a parallelogram having one of its interior angle as 90.
Hence, PQRS is rectangle.
Solution 3
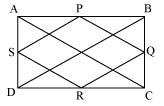
Let us join AC and BD
In ABC
ABC
P and Q are the mid-points of AB and BC respectively
 PQ || AC and PQ =
PQ || AC and PQ =  AC (mid point theorem) ... (1)
AC (mid point theorem) ... (1)
In
P and Q are the mid-points of AB and BC respectively
Similarly in
SR || AC and SR =
Clearly, PQ || SR and PQ = SR
As in quadrilateral PQRS one pair of opposite sides is equal and parallel to
each other, so, it is a parallelogram.
Now, in
But diagonals of a rectangle are equal
Now, by using equation (1), (2), (3), (4), (5) we can say that
PQ = QR = SR = PS
So, PQRS is a rhombus.
Solution 4
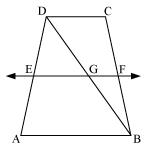
By converse of mid-point theorem a line drawn, through the mid point of any side of a triangle and parallel to another side bisects the third side.
Now in ABD
ABD
EF || AB and E is mid-point of AD
So, this line will intersect BD at point G and G will be the mid-point of DB.
Now as EF || AB and AB || CD
 EF || CD (Two lines parallel to a same line are parallel to each other)
EF || CD (Two lines parallel to a same line are parallel to each other)
Now in
EF || AB and E is mid-point of AD
So, this line will intersect BD at point G and G will be the mid-point of DB.
Now as EF || AB and AB || CD
Now, in  BCD, GF || CD and G is the midpoint of line BD. So, by using converse of mid-point theorem, F is the mid-point of BC.
BCD, GF || CD and G is the midpoint of line BD. So, by using converse of mid-point theorem, F is the mid-point of BC.
Solution 5
ABCD is a parallelogram
 AB || CD
AB || CD
So, AE || FC
Again AB = CD (opposite sides of parallelogram ABCD)
AE = FC (E and F are midpoints of side AB and CD)
As in quadrilateral AECF one pair of opposite sides (AE and CF) are parallel and equal to each other. So, AECF is a parallelogram.
Now, in
P is the mid-point of DQ
Similarly, in
Q is the mid-point of PB
From equations (1) and (2), we may say that
DP = PQ = BQ
Hence, the line segments AF and EC trisect the diagonal BD.
Solution 6
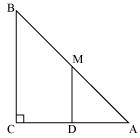
(i) In  ABC
ABC
Given that M is mid point of AB and MD || BC.
So, D is the mid-point of AC. (Converse of mid-point theorem)
(ii) As DM || CB and AC is a transversal line for them.
So, MDC +
MDC +  DCB = 180 (Co-interior angles)
DCB = 180 (Co-interior angles)
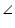 MDC + 90 = 180
MDC + 90 = 180
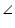 MDC = 90
MDC = 90
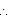 MD
MD 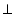 AC
AC
Given that M is mid point of AB and MD || BC.
So, D is the mid-point of AC. (Converse of mid-point theorem)
(ii) As DM || CB and AC is a transversal line for them.
So,
(iii) Join MC
In 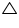 AMD and
AMD and 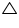 CMD
CMD
AD = CD (D is the midpoint of side AC)
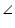 ADM =
ADM = 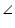 CDM (Each 90)
CDM (Each 90)
DM = DM (common)
 AMD
AMD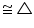 CMD (by SAS congruence rule)
CMD (by SAS congruence rule)
AD = CD (D is the midpoint of side AC)
DM = DM (common)
So, AM = CM (by CPCT)
But AM =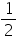 AB (M is mid point of AB)
AB (M is mid point of AB)
So, CM = MA =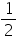 AB
AB
But AM =
So, CM = MA =
