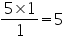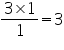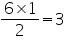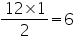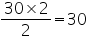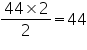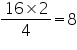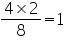Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

Class 9 NCERT Solutions Maths Chapter 12: Statistics

Statistics Exercise Ex. 12.1

Solution 1

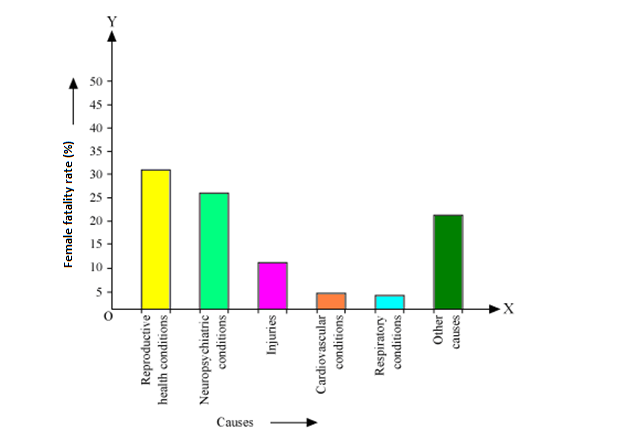
(i) By representing causes on x axis and family fatality rate on y axis and choosing an appropriate scale (1 unit = 5% for y axis) we can draw the graph of information given above, as following

          

All the rectangle bars are of same width and having equal spacing between them.

(ii) Reproductive health condition is the major cause of women's ill health and death worldwide as 31.8% of women are affected by it.      

Solution 2

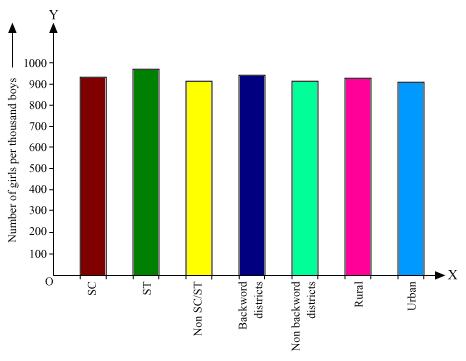
(i).    By representing section (variable) on x axis and number of girls per thousand boys on y axis we can draw the graph of information given as above and choosing an appropriate scale (1 unit = 100 girls for y axis)

 

Here all the rectangle bars are of same width and have equal spacing in between them.

Solution 3

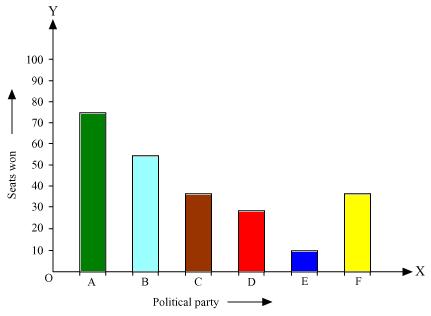
(i).    By taking polling results on x axis and seats won as y axis and choosing an appropriate scale (1 unit = 10 seats for y axis) we can draw the required graph of above information as below -

      

    Here rectangle bars are of same width  and have equal spacing in between them.  

(ii).    We may find that political party 'A' won maximum number of seats.

Solution 4

(i).    Length of leaves are represented in a discontinuous class intervals having a difference of 1 in between them. So we have to add   to each upper class limit and also have to subtract 0.5 from the lower class limits so as to make our class intervals continuous.
    

Length (in mm)

Number of leaves

117.5 - 126.5

3

126.5 - 135.5

5

135.5 - 144.5

9

144.5 - 153.5

12

153.5 - 162.5

5

162.5 - 171.5

4

171.5 - 180.5

2


Now taking length of leaves on x axis and number of leaves on y axis we can draw the histogram of this information as below -
 

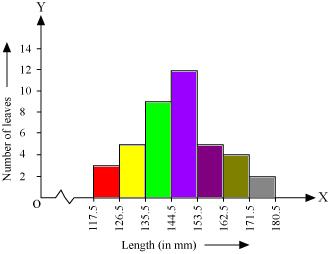
Here 1 unit on y axis represents 2 leaves.    

(ii).    Other suitable graphical representation of this data could be frequency polygon.  

(iii).    No as maximum number of leaves (i.e. 12) have their length in between of 144.5 mm and 153.5 mm. It is not necessary that all have their lengths as 153 mm.

Solution 5

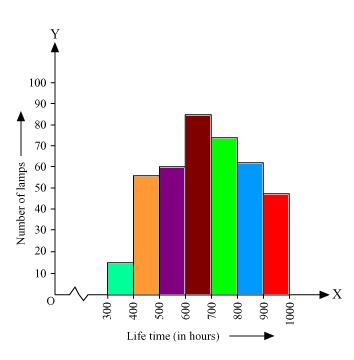
(i).    By taking life time (in hours) of neon lamps on x axis and number of lamps on y axis we can draw the histogram of the given information as below -
 
 
Here 1 unit on y axis represents 10 lamps.

(ii).    Number of neon lamps having their lifetime more than 700 are sum of number of neon lamps having their lifetime as   700 - 800, 800 - 900, and 900 - 1000.
So number of neon lamps having their lifetime more than 700 hours is 184. (74 + 62 + 48 = 184)

Solution 6

We can find class marks of given class intervals by using formula -

Class mark  
 
 
 

Section A

Section B

Marks

Class marks

Frequency

Marks

Class marks

Frequency

0 - 10

5

3

0 - 10

5

5

10 - 20

15

9

10 - 20

15

19

20 - 30

25

17

20 - 30

25

15

30 - 40

35

12

30 - 40

35

10

40 - 50

45

9

40 - 50

45

1
 
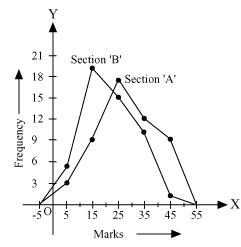
Now taking class marks on x axis and frequency on y axis and choosing an appropriate scale (1 unit = 3 for y axis) we can draw frequency polygon as below -

 

From the graph we can see performance of students of section 'A' is better than the students of section 'B' as for good marks.  

Solution 7

We observe that given data is not having its class intervals continuous. There is a gap of 1 in between of them. So we have to add  = 0.5  to upper class limits and subtract 0.5 from
lower class limits.
Also class mark of each interval can be found by using formula -
 
Class mark  
 

 
Now continuous data with class mark of each class interval can be represented as following -
 

Number of balls

Class mark

Team A

Team B

0.5 - 6.5

3.5

2

5

6.5 - 12.5

9.5

1

6

12.5 - 18.5

15.5

8

2

18.5 - 24.5

21.5

9

10

24.5 - 30.5

27.5

4

5

30.5 - 36.5

33.5

5

6

36.5 - 42.5

39.5

6

3

42.5 - 48.5

45.5

10

4

48.5 - 54.5

51.5

6

8

54.5 - 60.5

57.5

2

10


Now by taking class marks on x axis and runs scored on y axis we can construct frequency polygon as following -
 

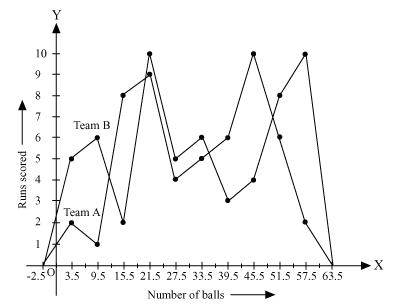
Solution 8

Here data is having class intervals of varying width. We may find proportion of children per 1 year interval as following -
   

Age (in years)

Frequency (Number of children)

Width of class

Length of rectangle

1 - 2

 

5

 

1

 

2 - 3

3

1

 

3 - 5

6

2

 

5 - 7

12

2

 

7 - 10

9

3

 

10 - 15

10

5

 

15 - 17

4

2

 


Now taking age of children on x axis and proportion of children per 1 year interval on y axis we may draw histogram as below -
 
 

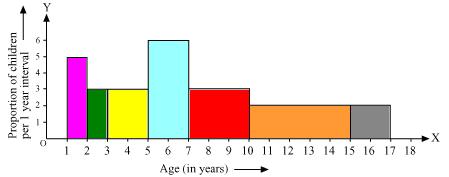
Solution 9

(i).    Given data is having class intervals of varying width. We need to compute the adjusted frequency

Number of letters

Frequency (Number of surnames)

Width of class

Length of rectangle

1 - 4

6

3

 

4 - 6

30

2

 

6 - 8

44

2

 

8 -12

16

4

 

12 - 20

4

8

 
                            

Now by taking number of letters on x axis and proportion of number of surnames per 2 letters interval on y axis and choosing an appropriate scale (1 unit = 4 students for y axis) we will construct the histogram as below

 


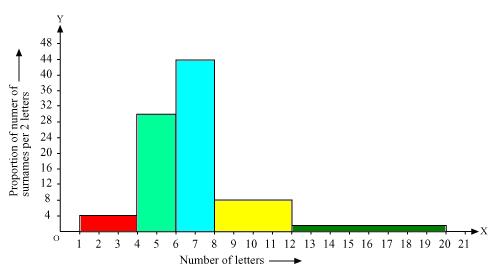
(ii).    The class interval in which the maximum number of surname lie is
6 - 8 as there are  44 number of surnames in it i.e. maximum for this data.  

My Class Videos Tests ₹ Plans Ask a Doubt