Class 9 NCERT Solutions Maths Chapter 11: Surface Areas and Volumes
Ex. 11.1
Ex. 11.2
Ex. 11.3
Ex. 11.4
Surface Areas and Volumes Exercise Ex. 11.1
Solution 1
Radius of base of cone = 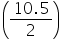 cm = 5.25 cm
cm = 5.25 cm
Slant height of cone = 10 cm
CSA of cone =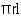 =
= 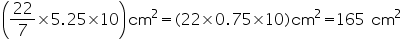
Thus, the curved surface area of cone is 165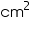 .
.
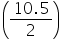 cm = 5.25 cm
cm = 5.25 cmSlant height of cone = 10 cm
CSA of cone =
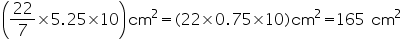
Thus, the curved surface area of cone is 165
Solution 2
Radius of base of cone = 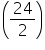 m = 12 cm
m = 12 cm
Slant height of cone = 21 m
Total surface area of cone =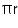 (r + l)
(r + l)
Slant height of cone = 21 m
Total surface area of cone =
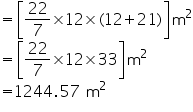
Solution 3
(i) Slant height of cone = 14 cm
Let radius of circular end of cone be r.
CSA of cone =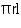
Let radius of circular end of cone be r.
CSA of cone =
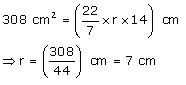
Thus, the radius of circular end of the cone is 7 cm.
(ii) Total surface area of cone = CSA of cone + Area of base
=
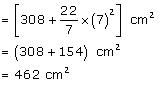
Thus, the total surface area of the cone is 462 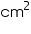 .
.
Solution 4
(i) Height (h) of conical tent = 10 m
Radius (r) of conical tent = 24 m
Let slant height of conical tent be l.
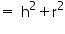
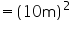

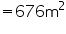
Radius (r) of conical tent = 24 m
Let slant height of conical tent be l.
.
Thus, the slant height of the conical tent is 26 m.
(ii) CSA of tent =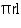 =
= 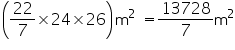
Cost of 1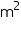 canvas = Rs 70
canvas = Rs 70
Cost of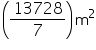 canvas =
canvas = 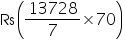 = Rs 137280
= Rs 137280
Thus, the cost of canvas required to make the tent is Rs 137280.
(ii) CSA of tent =
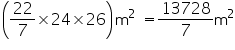
Cost of 1
Cost of
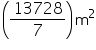 canvas =
canvas = 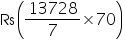 = Rs 137280
= Rs 137280Thus, the cost of canvas required to make the tent is Rs 137280.
Solution 5
Height (h) of conical tent = 8 m
Radius (r) of base of tent = 6 m
Slant height (l) of tent =
CSA of conical tent =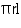 = (3.14
= (3.14 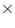 6
6 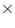 10)
10) 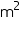 = 188.4
= 188.4 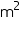
Let length of tarpaulin sheet required be L.
As 20 cm will be wasted so, effective length will be (L - 0.2 m)
Breadth of tarpaulin = 3 m
Area of sheet = CSA of tent
[(L - 0.2 m)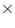 3] m = 188.4
3] m = 188.4 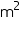
L - 0.2 m = 62.8 m
L = 63 m
Thus, the length of the tarpaulin sheet will be 63 m.
Radius (r) of base of tent = 6 m
Slant height (l) of tent =
CSA of conical tent =
Let length of tarpaulin sheet required be L.
As 20 cm will be wasted so, effective length will be (L - 0.2 m)
Breadth of tarpaulin = 3 m
Area of sheet = CSA of tent
[(L - 0.2 m)
L - 0.2 m = 62.8 m
L = 63 m
Thus, the length of the tarpaulin sheet will be 63 m.
Solution 6
Slant height (l) of conical tomb = 25 m
Base radius (r) of tomb = = 7 m
= 7 m
CSA of conical tomb =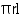 =
=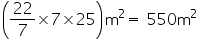
Cost of white-washing 100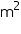 area = Rs 210
area = Rs 210
Cost of white-washing 550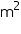 area =Rs
area =Rs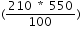 = Rs 1155
= Rs 1155
Thus, the cost of white washing the conical tomb is Rs 1155.
Base radius (r) of tomb =
CSA of conical tomb =
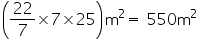
Cost of white-washing 100
Cost of white-washing 550
Thus, the cost of white washing the conical tomb is Rs 1155.
Solution 7
Radius (r) of conical cap = 7 cm
Height (h) of conical cap = 24 cm
Slant height (l) of conical cap =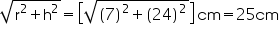
CSA of 1 conical cap =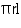 =
= 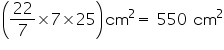
CSA of 10 such conical caps = (10 550)
550)  = 5500
= 5500 
Thus, 5500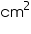 sheet will be required to make the 10 caps.
sheet will be required to make the 10 caps.
Height (h) of conical cap = 24 cm
Slant height (l) of conical cap =
CSA of 1 conical cap =
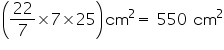
CSA of 10 such conical caps = (10
Thus, 5500
Solution 8
Radius (r) of cone =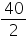 = 0.2 m
= 0.2 m
Height (h) of cone = 1 m
Height (h) of cone = 1 m
Slant height (l) of cone =
CSA of each cone =
CSA of 50 such cones = (50
Cost of painting 1
Cost of painting 32.028
Thus, it will cost Rs 384.34 (approximately) in painting the 50 hollow cones.
Surface Areas and Volumes Exercise Ex. 11.2
Solution 1
(i) Radius of sphere = 10.5 cm
Surface area of sphere = ![]()

(ii) Radius of sphere = 5.6 cm
Surface area of sphere = ![]() =
= 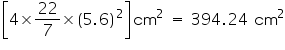
(iii) Radius of sphere = 14 cm
Surface area of sphere = ![]() =
= 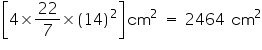
Solution 2
(i) Radius of sphere 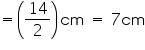
Surface area of sphere 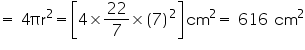
(ii) Radius of sphere 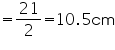
Surface area of sphere 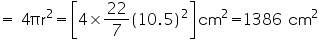
(iii) Radius of sphere 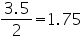
Surface area of sphere = ![]()
Solution 3
Radius of hemisphere = 10 cm
Total surface area of hemisphere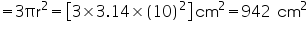
Total surface area of hemisphere
Solution 4
Radius 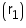 of spherical balloon = 7 cm
of spherical balloon = 7 cm
Radius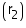 of spherical balloon, when air is pumped into it = 14 cm
of spherical balloon, when air is pumped into it = 14 cm
Radius
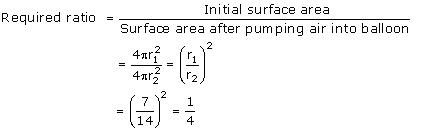
Solution 5
Inner radius (r) of hemispherical bowl = 
Surface area of hemispherical bowl =
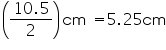
Surface area of hemispherical bowl =
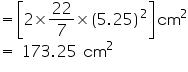
Cost of tin-plating 100
Cost of tin-plating 173.25
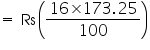 = Rs 27.72
= Rs 27.72Thus, the cost of tin-plating the inner side of hemispherical bowl is Rs 27.72
Solution 6
Let radius of the sphere be r.
Surface area of the sphere = 154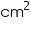
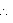
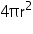 = 154 cm2
= 154 cm2
Surface area of the sphere = 154
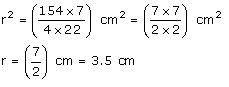
Thus, the radius of the sphere is 3.5 cm.
Solution 7
Let diameter of earth be d. Then, diameter of moon will be 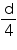 .
.
Radius of earth =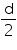
Radius of moon =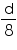
Surface area of moon =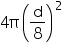
Surface area of earth =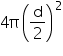
Required ratio =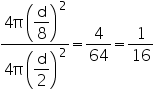
Thus, the required ratio of the surface areas is 1:16.
Radius of earth =
Radius of moon =
Surface area of moon =
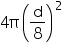
Surface area of earth =
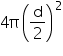
Required ratio =
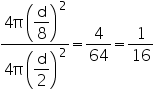
Thus, the required ratio of the surface areas is 1:16.
Solution 8
Inner radius of hemispherical bowl = 5 cm
Thickness of the bowl = 0.25 cm
 Outer radius (r) of hemispherical bowl = (5 + 0.25) cm = 5.25 cm
Outer radius (r) of hemispherical bowl = (5 + 0.25) cm = 5.25 cm
Outer CSA of hemispherical bowl =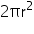
Thickness of the bowl = 0.25 cm
Outer CSA of hemispherical bowl =
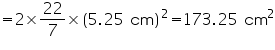
Thus, the outer curved surface area of the bowl is 173.25
Solution 9
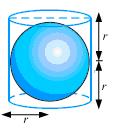
(i) Surface area of sphere = 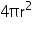
(ii) Height of cylinder = r + r = 2r
Radius of cylinder = r
CSA of cylinder =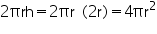
(iii) Required ratio =
(ii) Height of cylinder = r + r = 2r
Radius of cylinder = r
CSA of cylinder =
(iii) Required ratio =

Surface Areas and Volumes Exercise Ex. 11.3
Solution 1
(i) Radius (r) of cone = 6 cm
Height (h) of cone = 7 cm
Volume of cone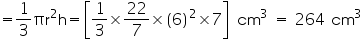
(ii) Radius (r) of cone = 3.5 cm
Height (h) of cone = 12 cm
Volume of cone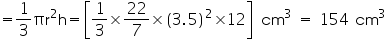
Height (h) of cone = 7 cm
Volume of cone
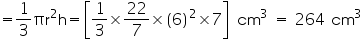
(ii) Radius (r) of cone = 3.5 cm
Height (h) of cone = 12 cm
Volume of cone
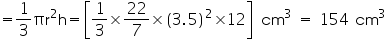
Solution 2
(i) Radius (r) of cone = 7 cm
Slant height (l) of cone = 25 cm
Height (h) of cone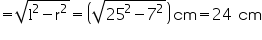
Volume of cone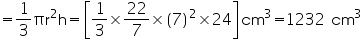
Capacity of the conical vessel =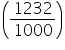 litres= 1.232 litres
litres= 1.232 litres
Slant height (l) of cone = 25 cm
Height (h) of cone
Volume of cone
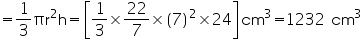
Capacity of the conical vessel =
 litres= 1.232 litres
litres= 1.232 litres(ii) Height (h) of cone = 12 cm
Slant height (l) of cone = 13 cm
Radius (r) of cone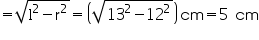
Volume of cone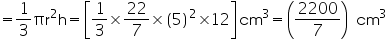
Capacity of the conical vessel =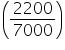 litres =
litres = 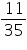 litres.
litres.
Slant height (l) of cone = 13 cm
Radius (r) of cone
Volume of cone
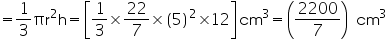
Capacity of the conical vessel =
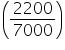 litres =
litres = Solution 3
Height (h) of cone = 15 cm
Let radius of cone be r.
Volume of cone = 1570 cm3
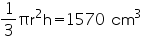
Let radius of cone be r.
Volume of cone = 1570 cm3
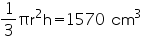
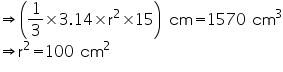
r = 10 cm
Thus, the radius of the base of the cone is 10 cm.
Thus, the radius of the base of the cone is 10 cm.
Solution 4
Height (h) of cone = 9 cm
Let radius of cone be r.
Volume of cone = 48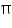 cm3
cm3
Let radius of cone be r.
Volume of cone = 48
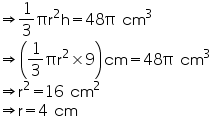
Thus, the diameter of the base of the cone is 2r = 8 cm.
Solution 5
Radius (r) of pit =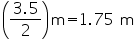
Depth (h) of pit = 12 m
Volume of pit =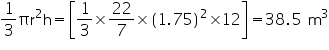 = 38.5 m3
= 38.5 m3
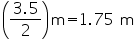
Depth (h) of pit = 12 m
Volume of pit =
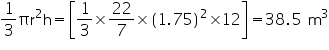 = 38.5 m3
= 38.5 m3Solution 6
(i) Radius of cone = 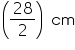 =14 cm
=14 cm
Let height of cone be h.
Volume of cone = 9856 cm3
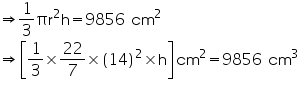
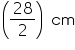 =14 cm
=14 cmLet height of cone be h.
Volume of cone = 9856 cm3
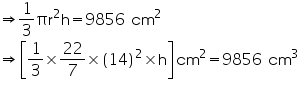
h = 48 cm
Thus, the height of the cone is 48 cm.
(ii) Slant height (l) of cone 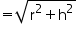

Thus, the slant height of the cone is 50 cm.
(iii) CSA of cone = 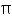 rl=
rl= 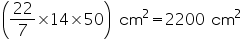 = 2200 cm2
= 2200 cm2
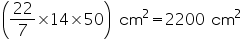 = 2200 cm2
= 2200 cm2Solution 7
When the right angled  ABC is revolved about its side 12 cm, a cone of height (h) 12 cm, radius (r) 5 cm, and slant height (l) 13 cm will be formed.
ABC is revolved about its side 12 cm, a cone of height (h) 12 cm, radius (r) 5 cm, and slant height (l) 13 cm will be formed.
Volume of cone = 100
= 100 cm3
cm3
Thus, the volume of cone so formed by the triangle is 100 cm3.
cm3.
Volume of cone
 = 100
= 100Thus, the volume of cone so formed by the triangle is 100
Solution 8
When the right angled 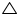 ABC is revolved about its side 5 cm, a cone of radius (r) 12 cm, height (h) 5 cm, and slant height (l) 13 cm will be formed.
ABC is revolved about its side 5 cm, a cone of radius (r) 12 cm, height (h) 5 cm, and slant height (l) 13 cm will be formed.
Volume of cone =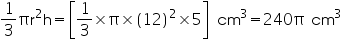
Volume of cone =
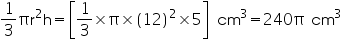
Required ratio 

Solution 9
Radius (r) of heap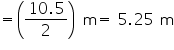
Height (h) of heap = 3 m
Volume of heap=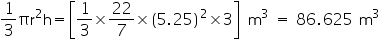
Slant height (l) =
Area of canvas required = CSA of cone
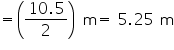
Height (h) of heap = 3 m
Volume of heap=
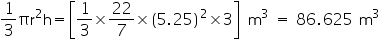
Slant height (l) =
Area of canvas required = CSA of cone
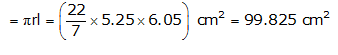
Surface Areas and Volumes Exercise Ex. 11.4
Solution 1
(i) Radius of sphere = 7 cm
Volume of sphere =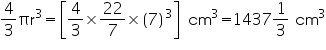
Volume of sphere =
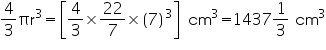
(ii) Radius of sphere = 0.63 m
Volume of sphere =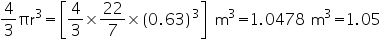
Volume of sphere =
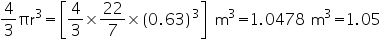
m3(approximately)
Solution 2
(i) Radius (r) of ball = 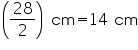
Volume of ball =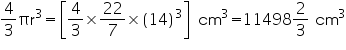
Thus, the amount of water displaced is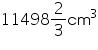 .
.
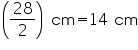
Volume of ball =
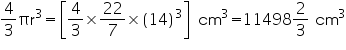
Thus, the amount of water displaced is
 .
.(ii) Radius (r) of ball =  = 0.105 m
= 0.105 m
Volume of ball =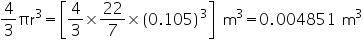
Thus, the amount of water displaced is 0.004851 m3.
 = 0.105 m
= 0.105 mVolume of ball =
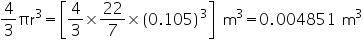
Thus, the amount of water displaced is 0.004851 m3.
Solution 3
Radius (r) of metallic ball = 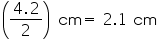
Volume of metallic ball =
Mass = Density Volume = (8.9 * 38.808) g = 345.3912 g
Volume = (8.9 * 38.808) g = 345.3912 g
Thus, the mass of the ball is approximately 345.39 g.
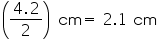
Volume of metallic ball =

Mass = Density
Thus, the mass of the ball is approximately 345.39 g.
Solution 4
Let diameter of earth be d. So, radius earth will be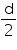 .
.
Then, diameter of moon will be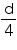 . So, radius of moon will be
. So, radius of moon will be 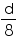 .
.
Volume of moon =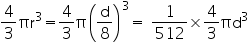
Volume of earth =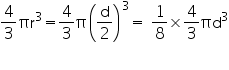
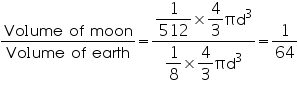
Thus, the volume of moon is of volume of earth.
of volume of earth.
Then, diameter of moon will be
Volume of moon =
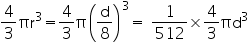
Volume of earth =
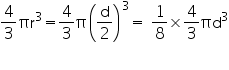
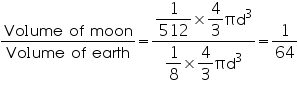
Thus, the volume of moon is
Solution 5
Radius (r) of hemispherical bowl =  = 5.25 cm
= 5.25 cm
 = 5.25 cm
= 5.25 cmVolume of hemispherical bowl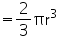
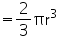
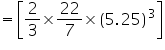
= 303.1875 cm3
Capacity of the bowl
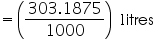
= 0.3031875 litre = 0.303 litre (approximately)
Thus, the hemispherical bowl can hold 0.303 litre of milk.
Solution 6
Inner radius (r1) of hemispherical tank = 1 m
Thickness of hemispherical tank = 1 cm = 0.01 m
Outer radius (r2) of hemispherical tank = (1 + 0.01) m = 1.01 m
Thickness of hemispherical tank = 1 cm = 0.01 m
Outer radius (r2) of hemispherical tank = (1 + 0.01) m = 1.01 m
Volume of iron used to make the tank = 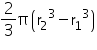
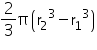

Solution 7
Let the radius of the sphere be r.
Surface area of sphere = 154 cm2
 r2 = 154 cm2
r2 = 154 cm2
Surface area of sphere = 154 cm2
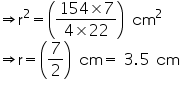
Volume of sphere
Solution 8
(i) Cost of white washing the dome from inside = Rs 498.96
Cost of white washing 1 m2 area = Rs 2
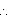 CSA of inner side of dome =
CSA of inner side of dome = 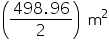 = 249.48 m2
= 249.48 m2
Cost of white washing 1 m2 area = Rs 2
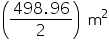 = 249.48 m2
= 249.48 m2(ii) Let inner radius of hemispherical dome be r.
CSA of inner side of dome = 249.48 m2
2 r2 = 249.48 m2
r2 = 249.48 m2

Volume of air inside the dome = Volume of the hemispherical dome
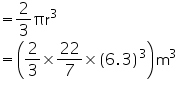
= 523.908 m3
Thus, the volume of air inside the dome is approximately 523.9 m3.
CSA of inner side of dome = 249.48 m2
2

Volume of air inside the dome = Volume of the hemispherical dome
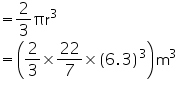
= 523.908 m3
Thus, the volume of air inside the dome is approximately 523.9 m3.
Solution 9
(i) Radius of 1 solid iron sphere = r
Volume of 1 solid iron sphere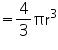
Volume of 27 solid iron spheres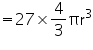
It is given that 27 sold iron spheres are melted to from 1 iron sphere. So, volume of
Volume of 1 solid iron sphere
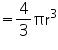
Volume of 27 solid iron spheres
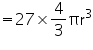
It is given that 27 sold iron spheres are melted to from 1 iron sphere. So, volume of
this iron sphere will be equal to volume of 27 solid iron spheres.
Radius of the new sphere = r'.
Volume of new sphere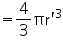
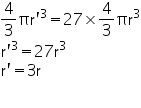
Radius of the new sphere = r'.
Volume of new sphere
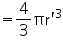
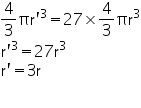
(ii) Surface area of 1 solid iron sphere of radius r = 4 r2
r2
Surface area of iron sphere of radius r' = 4 (r')2 = 4
(r')2 = 4  (3r)2 = 36
(3r)2 = 36  r2
r2
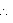
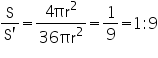
Surface area of iron sphere of radius r' = 4
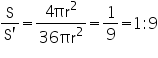
Solution 10
Radius (r) of capsule
Volume of spherical capsule
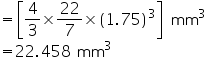
Thus, approximately 22.46 mm3 of medicine is required to fill the capsule.

Volume of spherical capsule

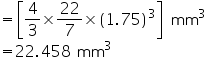
Thus, approximately 22.46 mm3 of medicine is required to fill the capsule.
